Question

Consider the probability that greater than 100 out of 151 students will pass their college placement exams. Assume the probability that a given student will pass their college placement exam is 64%. Approximate the probability using the normal distribution. Round your answer to four decimal places.

Answer 1

0.3137 is the probability that more than 100 students will pass the college placement exam.

Explanation:

We are given the following in the question:

Sample size, n = 151

probability student will pass their college placement exam = 64%

`p = 0.64`

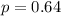
Formula:

`\mu = np = 151(0.64) = 96.64\\\sigma = √(np(1-p)) = √(151(0.64)(1-0.64)) = 5.89`

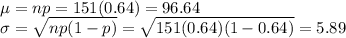
We have to evaluate

P(x > 100)

Formula:

`z_(score) = \displaystyle(x-\mu)/(\sigma)`

`P( x > 100) = P(100-0.5) = P( z > \displaystyle(99.5 - 96.64)/(5.89))\\\\ = P(z > 0.4855)`

`= 1 - P(z \leq 0.4855)`

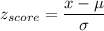
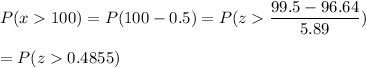
Calculation the value from standard normal z table, we have,

`P(x >99.5) = 1 - 0.6863 =0.3137 = 31.37\%`

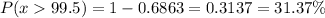
0.3137 is the probability that more than 100 students will pass the college placement exam.