Question

Consider the reaction 4HCl(g) + O2(g)2H2O(g) + 2Cl2(g) Using standard thermodynamic data at 298K, calculate the entropy change for the surroundings when 2.27 moles of HCl(g) react at standard conditions. Ssurroundings = J/K

Answer 1

Answer: The value of
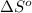`\Delta S^o` for the surrounding when given amount of HCl gas is reacted is 73.21 J/K

Step-by-step explanation:

Entropy change is defined as the difference in entropy of all the product and the reactants each multiplied with their respective number of moles.

The equation used to calculate entropy change is of a reaction is:

`\Delta S^o_(rxn)=\sum [n* \Delta S^o_((product))]-\sum [n* \Delta S^o_((reactant))]`

For the given chemical reaction:

`4HCl(g)+O_2(g)\rightarrow 2H_2O(g)+2Cl_2(g)`

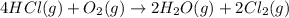
The equation for the entropy change of the above reaction is:

`\Delta S^o_(rxn)=[(2* \Delta S^o_((Cl_2(g))))+(2* \Delta S^o_((H_2O(g))))]-[(4* \Delta S^o_((HCl(g))))+(1* \Delta S^o_((O_2(g))))]`

We are given:

`\Delta S^o_((O_2(g)))=205.14J/K.mol\\\Delta So_((HCl(g)))=186.91J/K.mol\\\Delta S^o_((Cl_2(g)))=223.07J/K.mol\\\Delta S^o_((H_2O(g)))=188.82J/K.mol`

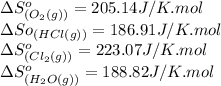
Putting values in above equation, we get:

`\Delta S^o_(rxn)=[(2* (223.07))+(2* (188.82))]-[(4* (186.91))+(1* (205.14))]\\\\\Delta S^o_(rxn)=-129J/K`

Entropy change of the surrounding = - (Entropy change of the system) = -(-129) J/K = 129 J/K

We are given:

Moles of HCl gas reacted = 2.27 moles

By Stoichiometry of the reaction:

When 4 mole of HCl gas is reacted, the entropy change of the surrounding will be 129 J/K

So, when 2.27 moles of HCl gas is reacted, the entropy change of the surrounding will be =
`(129)/(4)* 2.27=73.21J/K`

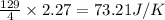
Hence, the value of
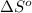`\Delta S^o` for the surrounding when given amount of HCl gas is reacted is 73.21 J/K