Answer:
Part A
it would take 6 sec
it would take 3 sec
Step-by-step explanation:
We are told that the power supplied to the wheel is constant which means that the sport car is gaining energy i.e
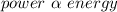
Hence if power is constantly supplied energy constantly increase
From the formula of the Kinetic energy
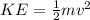
we can see that as the speed doubles from 29 mph to 58 mph the energy needed is
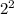 = 4 times of the energy from the formula
= 4 times of the energy from the formula
Also the time needed would also be 4 times because energy i directly proportional to time
Hence to reach 58mph the time that it would take is
=
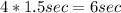
We are told that the ground pushes the car with a constant force and
F = ma
this means that the acceleration is also constant
now from newtons law
v = u +at
Looking at it we see that final velocity is directly proportional with time
hence it would take twice the time to reach twice the final velocity
Time to reach 58mph = 3 s
since time to reach 29 mph(
![(1)/(2) \ of \ [58mph]](https://img.qammunity.org/2021/formulas/physics/college/cz2x30xckucrycf7yk6ut5959yb5rqu0y5.png) ) =(
) =(
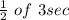 )1.5 s
)1.5 s