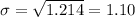Answer:
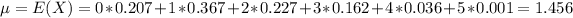
For the variance we need to calculate first the second moment given by:

And replacing we got:
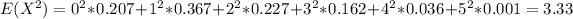
And the variance is given by:
![\sigma^2 = E(X^2) - [E(X)]^2 = 3.334 -[1.456]^2 =1.21](https://img.qammunity.org/2021/formulas/mathematics/college/n2bs29ykfkrvyanasgdwofu79g4ea7t20c.png)
And the deviation is:
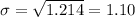
Explanation:
For thi case we have the following distribution given:
X 0 1 2 3 4 5
P(X) 0.207 0.367 0.227 0.162 0.036 0.001
For this case the expected value is given by:
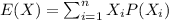
And replacing we got:
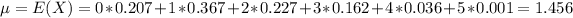
For the variance we need to calculate first the second moment given by:

And replacing we got:
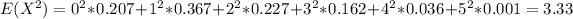
And the variance is given by:
![\sigma^2 = E(X^2) - [E(X)]^2 = 3.334 -[1.456]^2 =1.21](https://img.qammunity.org/2021/formulas/mathematics/college/n2bs29ykfkrvyanasgdwofu79g4ea7t20c.png)
And the deviation is: