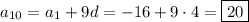Question

The sum of the sixth and ninth terms of an arithmetic sequence is 20 and the product of the sixth and ninth terms is 64. Find the tenth term in the sequence if the first term in the sequence is negative.

Answer 1

Let
`a_n` denote the
`n`th term in the sequence. Then

`a_n=a_(n-1)+d`

`a_n=(a_(n-2)+d)+d=a_(n-2)+2d`

`a_n=(a_(n-3)+d)+2d=a_(n-3)+3d`

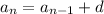
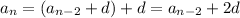
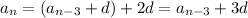
and so on down to

`a_n=a_1+(n-1)d`

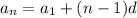
where
`d` is the common difference between terms in the sequence.

This means we have

`a_6=a_1+5d`

`a_9=a_1+8d`

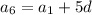
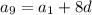
Given that
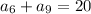`a_6+a_9=20` and
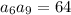`a_6a_9=64`, we can substitute the relationships above to solve for
`a_1`:

`\begin{cases}(a_1+5d)+(a_1+8d)=20\\(a_1+5d)(a_1+8d)=64\end{cases}`

`\implies\begin{cases}2a_1+13d=20\\{a_1}^2+13a_1d+40d^2=64\end{cases}`

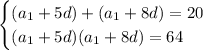
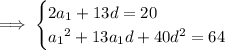
From the first equation, we get

`d=(20-2a_1)/(13)`

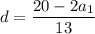
Substitute this into the second equation and solve for
`a_1`:

`{a_1}^2+a_1(20-2a_1)+(40)/(169)(20-2a_1)^2=64`

`\implies{a_1}^2-20a_1-576=(a_1-36)(a_1+16)=0`

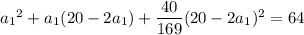
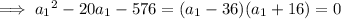
from which it follows that the first term is
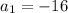`a_1=-16` (because we're told it's negative).

Then the common difference is
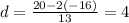`d=(20-2(-16))/(13)=4`, and so the 10th term in the sequence is

`a_(10)=a_1+9d=-16+9\cdot4=\boxed{20}`