Question

Early black-and-white television sets used an electron beam to draw a picture on the screen. The electrons in the beam were accelerated by a voltage of 3.0 kV; the beam was then steered to different points on the screen by coils of wire that produced a magnetic field of up to 0.66 T .

a. What is the speed of electrons in the beam?
b. What acceleration do they experience due to the magnetic field, assuming that it is perpendicular to their path? What is this acceleration in units of g ?
c. If the electrons were to complete a full circular orbit, what would be the radius?

Answer 1

speed of electrons = 3.25 ×
`10^(7)` m/s

acceleration in term g is 3.9 ×
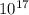`10^(17)` g.

radius of circular orbit is 2.76 ×
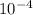`10^(-4)` m

Step-by-step explanation:

given data

voltage = 3 kV

magnetic field = 0.66 T

solution

law of conservation of energy

PE = KE

qV = 0.5 × m × v²

v =
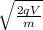
`\sqrt{(2qV)/(m)}`

v =
`\sqrt{(2* 1.6 * 10^(-19)* 3)/(9.1* 10^(-31))`

v = 3.25 ×
`10^(7)` m/s

and

magnetic force on particle movie in magnetic field

F = Bqv

ma = Bqv

a =
`(Bqv)/(m)`

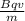
a =
`(0.67* 1.6* 10^(-19)* 3.25* 10^7)/(9.1* 10^(-31))`

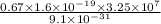
a = 3.82 ×
`10^(18)` m/s²

and acceleration in term g

a =
`(3.82* 10^(18))/(9.81)`

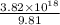
a = 3.9 ×
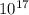`10^(17)` g

acceleration in term g is 3.9 ×
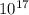`10^(17)` g.

and

electron moving in circular orbit has centripetal force

F =
`(mv^2)/(r)`

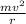
Bqv =
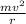
`(mv^2)/(r)`

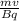
r =
`(mv)/(Bq)`

r =
`(9.1* 10^(-31)* 3.25* 10^7)/(0.67* 1.6* 10^(-19))`

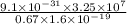
r = 2.76 ×
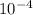`10^(-4)` m

radius of circular orbit is 2.76 ×
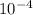`10^(-4)` m