Answer:
1.74%
Step-by-step explanation:
Mean number of hours (μ) = 2,220 hours
Standard deviation (σ) = 285 hours
Assuming a normal distribution, the z-score for any number of hours a network stays up, X, is given by:
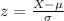
For X = 2,800 hours, the z-score is:
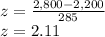
A z-score of 2.11 corresponds to the 98.26th percentile of a normal distribution. The probability that the network will stay up for 2,800 hours before it fails is:
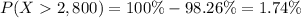
The probability is 1.74%.