Question

A brewery filling machine is adjusted to fill quart bottles with a mean of 32 ounces of ale and a variance of 0.003 ounces2. Periodically, a bottle is checked, and the amount of ale is noted. Assuming the amount of fill is normally distributed, what is the probability that the next randomly checked bottle contains less than 31.9 ounces?

Answer 1

The probability is about 0.03438 or 3.438%.

Explanation:

We are going to use the standard normal table to consult the associated probability and we need to find the z-score for the raw value of 31.9 ounces.

The formula for z-scores is as follows:

`\\ z = (x - \mu)/(\sigma)` (1)

Where

`\\ x\;is\;the\;raw\;score`.

`\\ \mu\;is\;the\;population\;mean`.

`\\ \sigma\;is\;the\;population\;standard\;deviation`.

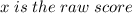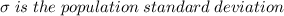The amount of fill is normally distributed with a mean of 32 ounces and a variance of
`\\ 0.003\;ounces^(2)`. We already know that the parameters of the normal distribution are the mean and the standard deviation. The standard deviation is

`\\ \sigma = √(variance) = \sigma = √(0.003) = 0.05477 \approx 0.055`

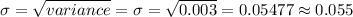
The probability that the next randomly checked bottle contains less than 31.9 ounces

We need to apply the formula (1) to find the z-score related to the raw score of x = 31.9 ounces. With this value at hand, we can consult the standard normal table to find the probability for that z-score in a standard normal distribution (with mean = 0 and standard deviation = 1).

`\\ \mu = 32\;ounces`

`\\ \sigma = 0.055\;ounces`

`\\ x = 31.9\;ounces`

`\\ z = (x - \mu)/(\sigma)`

`\\ z = (31.9 - 32)/(0.055)`

`\\ z = -1.818181... \approx -1.82`

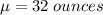
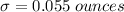
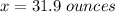
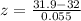
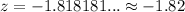
Since the standard normal table only gives us positive values for z (scores above the mean), we can determine the probability for z = -1.82 using the fact that the normal distribution is symmetrical (z = -1.82 and z = 1.82 are at the same distance from the mean but in different directions).

Then

`\\ P(z<-1.82) = 1 - P(z<1.82) = P(z>1.82)`

`\\ P(z<-1.82) = 1 - 0.96562 = P(z>1.82)`

`\\ P(z<-1.82) = 0.03438 = P(z>1.82)`

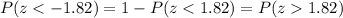
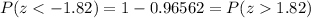
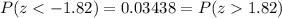
Thus, 'the probability that the next randomly checked bottle contains less than 31.9 ounces' is about 0.03438 or 3.438%.

The graph below shows this probability (notice that it is a standard normal distribution (mean = 0 and standard deviation = 1) that serves us to find the probability of a raw value from a normal distribution with mean = 32 and standard deviation of 0.055, approximately). Also notice the influence of the small value of the standard deviation in the result.

Note: without rounding the value of the standard deviation the probability is about 0.03362 or 3.362%.