Answer:
8, 15 and 17 feet respectively
Explanation:
Let the shorter leg=l feet
The longer leg of a right triangle is 7 ft longer than the shorter leg, therefore Length of the longer leg=(l+7) feet
The hypotenuse is 9ft longer than the shorter leg. Therefore Length of the hypotenuse=(l+9) feet
Using Pythagoras Theorem
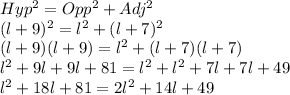
This results into:
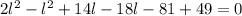
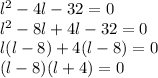
l-8=0 or l+4=0
l=8 or -4
Since length cannot be negative, The length l=8 feet
The sides of the rectangle are therefore: 8, 15 and 17 feet respectively