Question

The longer leg of a right triangle is 7 ft longer than the shorter leg. The hypotenuse is 9ft longer than the shorter leg. Find the side lengths of the triangle.

Answer 1

8, 15 and 17 feet respectively

Explanation:

Let the shorter leg=l feet

The longer leg of a right triangle is 7 ft longer than the shorter leg, therefore Length of the longer leg=(l+7) feet

The hypotenuse is 9ft longer than the shorter leg. Therefore Length of the hypotenuse=(l+9) feet

Using Pythagoras Theorem

`Hyp^2=Opp^2+Adj^2\\(l+9)^2=l^2+(l+7)^2\\(l+9)(l+9)=l^2+(l+7)(l+7)\\l^2+9l+9l+81=l^2+l^2+7l+7l+49\\l^2+18l+81=2l^2+14l+49`

This results into:

`2l^2-l^2+14l-18l-81+49=0`

`l^2-4l-32=0\\l^2-8l+4l-32=0\\l(l-8)+4(l-8)=0\\(l-8)(l+4)=0`

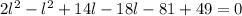
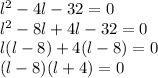
l-8=0 or l+4=0

l=8 or -4

Since length cannot be negative, The length l=8 feet

The sides of the rectangle are therefore: 8, 15 and 17 feet respectively