Question

Do well-rounded people get fewer colds?

A study on the Chronicle of Higher Education was conducted by scientists at Carnegie Mellon University, the University of Pittsburgh and the University of Virginia. They found that people who have only a few social outlets get more colds than those who are involved in a variety of social activities. Suppose that of the 276 healthy men and women tested, n1= 96 had only a few social outlets and n2 = 105 were busy with six or more activities. When these people were exposed to a cold virus, the following results were observed:Few social outlets: 62% with coldsMany social outlets: 35% with coldsa) Construct a 99% confidence interval for the difference in the two population proportionsb) You might think that coming into contact with more people would lead to more colds but the data show the opposite effect. How can you explain this unexpected finding ?

Answer 1

Explanation:

Hello!

The objective is to test if people with less social contact get more colds than people who are involved in a variety of social activities.

For this, a sample of 276 healthy men and women was taken.

n₁= 96 had few social outlets

n₂= 105 had six or more activities

These two groups were exposed to the cold virus and the following proportions of individuals that got sick were obtained:

p'₁= 0.62 (62% of the people with few social outlets got sick)

p'₂= 0.35 (35% of the people with six or more activities got sick)

The study variables are X₁: number of people with few social outlets that got sick after being exposed to the cold virus, in a sample of 96, and X₂: number of people with six or more activities that got sick after being exposed to the cold virus, in a sample of 105.

You have to construct a 99% CI for the difference these two populations since there is no specific order given I'll estimate: p₁ - p₂

(p'₁ - p'₂) ±
`Z_(1-\alpha /2) * \sqrt{(p'_1(1-p'_1))/(n_1) +(p'_2(1-p'_2))/(n_2) }`

`Z_(1-\alpha /2)= Z_(0.995)= 2.586`

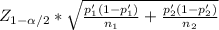
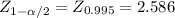
(0.62-0.35) ± 2.586
`\sqrt{(0.62*0.38)/(96) +(0.35*0.65)/(105) }`

[0.094; 0.045]

With a 99% confidence level, you'd expect that the difference between the proportion of people with few social outlets that got sick and the proportion of people with six or more social activities that got sick after being exposed to the cold virus.

I hope it helps!