Question

An unwary football player collides with a padded goalpost while running at a velocity of 9.50 m/s and comes to a full stop after compressing the padding and his body 0.250 m.

(a) How long does the collision last?
(b) What is his deceleration?

Answer 1

(a) The collision lasts for 0.053 s.

(b) The deceleration is 180.5 m/s².

Step-by-step explanation:

Given:

Initial velocity of the player (u) = 9.50 m/s

Final velocity of the player (v) = 0 m/s (Comes to a stop)

Displacement of the player (S) = 0.250 m

We know that, using equation of motion relating displacement (S), acceleration (a), initial velocity (u) and final velocity (v), we have:

`v^2=u^2+2aS`

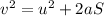
Expressing in terms of 'a', we get:

`a=(v^2-u^2)/(2S)`

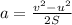
Plug in the given values and solve for 'a'. This gives,

`a=(0-9.50^2)/(2* 0.250)\\\\a=(-90.25)/(0.5)=-180.5\ m/s^2`

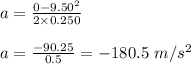
Therefore, the acceleration of the player is -180.5 m/s². So, the deceleration is 180.5 m/s².

Now, using the first equation of motion, we have:

`v=u+at\\\\t=(v-u)/(a)`

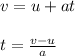
Plug in the given values and solve for 't'. This gives,

`t=(0-9.5)/(-180.5)\\\\t=0.053\ s`

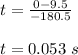
Therefore, the the collision will last for 0.053 s.

(a) The collision lasts for 0.053 s.

(b) The deceleration is 180.5 m/s².