Answer:
(a) The collision lasts for 0.053 s.
(b) The deceleration is 180.5 m/s².
Step-by-step explanation:
Given:
Initial velocity of the player (u) = 9.50 m/s
Final velocity of the player (v) = 0 m/s (Comes to a stop)
Displacement of the player (S) = 0.250 m
We know that, using equation of motion relating displacement (S), acceleration (a), initial velocity (u) and final velocity (v), we have:
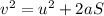
Expressing in terms of 'a', we get:
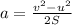
Plug in the given values and solve for 'a'. This gives,
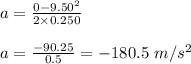
Therefore, the acceleration of the player is -180.5 m/s². So, the deceleration is 180.5 m/s².
Now, using the first equation of motion, we have:
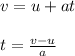
Plug in the given values and solve for 't'. This gives,
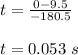
Therefore, the the collision will last for 0.053 s.
(a) The collision lasts for 0.053 s.
(b) The deceleration is 180.5 m/s².