Question

Suppose that 75% of all trucks undergoing a brake inspection at a certain inspection facility pass the inspection. Consider groups of 15 trucks and let X be the number of trucks in a group that have passed the nspection Part a: Verify that this is a binomial distribution Part b: For what proportion of groups will between 8 and 10 trucks (inclusive) pass the inspection? Part c: For what proportion of groups will exactly 3 trucks fail the inspection? Part d: Find the mean and the standard deviation of the random variable X

Answer 1

b) 0.2961

c) 0.2251

d) Mean = 11.25, Standard deviation = 1.667

Explanation:

We are given the following information:

We treat trucks undergoing a brake inspection passin as a success.

P( trucks undergoing a brake inspection passes the test) = 75% = 0.75

a) Conditions for binomial probability distribution

1. There are n independent trial.
2. Each trial have a success probability p
3. The probability of success is same for all trials.

Then the number of trucks undergoing a brake inspection follows a binomial distribution, where

`P(X=x) = \binom{n}{x}.p^x.(1-p)^(n-x)`

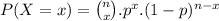
where n is the total number of observations, x is the number of success, p is the probability of success.

Now, we are given n = 15

b) P(proportion of groups will between 8 and 10 trucks pass the inspection)

We have to evaluate:

`P(8\leq x \leq 10) = P(x = 8) + P(x = 9) + P(x = 10)\\= \binom{15}{8}(0.75)^8(1-0.75)^7 + \binom{15}{9}(0.75)^9(1-0.75)^6 + \binom{15}{10}(0.75)^(10)(1-0.75)^5\\= 0.0393 + 0.0917 + 0.1651\\= 0.2961`

c) P( exactly 3 trucks fail the inspection)

p = 0.25

`P(x = 3)\\= \binom{15}{3}(0.25)^3(1-0.25)^(12)\\=0.2251`

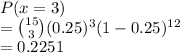
d) Mean and standard deviation

`\mu = np = 15(0.75) = 11.25\\\sigma = √(np(1-p)) = √(15(0.75)(1-0.75)) = 1.667`