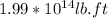Question

A Pyramid is 600 ft high (due to erosion, its current height is slightly less) and has a square base of side 5400 ft. Find the work needed to build the pyramid if the density of the stone is estimated at 228 lb/ft3.

Answer 1

Work needed to build the pyramid =
`1.99*10^(14)lb.ft`

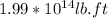
Explanation:

Let us consider a pyramid with a square base of length b and a height h. The pyramid has a density of x' pounds per cubic foot. Let's say that we make a thin slice through the pyramid at height y above the base, since the base of the pyramid is square, the slice will be a square of side length x. Since all of the material in that slice is at the same height, the amount of work needed to lift that slice into position would be

`p(volume`
`of`
`slice) /y = p(x^2dy)/y`

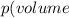
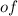
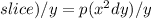
An argument with similar triangles shows that

`x=(b)/(h) (h-y)`

Hence, the total work needed to build the pyramid is

`\int\limits^h_0p(b^2)/(h^2) (h-y)^2ydy=p (b^2)/(h^2)\int\limits^h_0h^2y-2hy^2+y^3dy\\=p(b^2)/(h^2) ((h^2)/(2)y^2-(2h)/(3)y^3+(1)/(4)y^4)|0^h\\=(1)/(12) p b^2 h^2=(1)/(12)*228*(5400)^2*(600)^2`

≅
`1.99*10^(14)lb.ft`