Question

The friends are ready to try a problem. A battery has an emf of 12.0 V and an internal resistance of 0.05 Ω. Its terminals are connected to a load resistance of 1.1 Ω. Find the terminal voltage of the battery. V Calculate the power delivered to the load resistor, the power delivered to the internal resistance of the battery, and the power delivered by the battery. PR = W Or = W Delivered by battery = W

Answer 1

Terminal voltage = 11.5 V

Power across load = 119.7 W

Power across internal resistance = 5.4 W

Power delivered by battery = 125.2 W

Step-by-step explanation:

The current in the circuit is given by

`I=(E)/(R+r)`

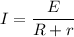
where E is the emf of the battery, R us the load resistance and r is the internal resistance.

`I=(12)/(1.1+0.05) = 10.43 \text{ A}`

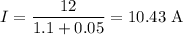
The terminal voltage is the potential difference across the load resistor.

V = I × R = 10.43 A × 1.1 Ω = 11.5 V

The power across any resistance is given by
`I^2R`

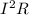
For the load resistor,

`P_L=10.43^2*1.1 = 119.7 \text{ W}`

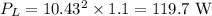
For the internal resistance,

`P_r=10.43^2*0.05= 5.4\text{ W}`

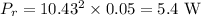
The power delivered by the battery is

`P = P_L + P_r = 119.7 + 5.4 = 124.1 \text{ W}`

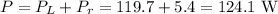
This could also be found by

`P = IE = 10.34*12 = 125.2 \text{ W}`

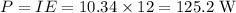
The discrepancy in both answers is due to the approximations. The second answer is better.