Question

The mammogram is helpful for detecting breast cancer in its early stages. However, it is an imperfect diagnostic tool. According to one study,11 86.6 of every 1000 women between the ages of 50 and 59 that do not have cancer are wrongly diagnosed (a "false positive"), while 1.1 of every 1000 women between the ages of 50 and 59 that do have cancer are not diagnosed (a "false negative"). One in 38 women between 50 and 59 will develop breast cancer. If a woman between the ages of 50 and 59 has a positive mammogram, what is the probability that she will have breast cancer?

Answer 1

The probability that she will have breast cancer is 0.2375.

Explanation:

P(Positive if no Cancer) = 86.6/1000 = 0.0866

P(Positive if Cancer) = 1 − 1.1/1000 = 0.9989, and

P(Cancer) = 1/38 = 0.0263

If a woman between the ages of 50 and 59 has a positive mammogram, the probability that she will have breast cancer will be calculated by using the Bayes rule.

Bayes’s theorem describes the probability of an event.

P(Cancer if Positive) =
`(P(Cancer)P(Positive if Cancer))/(P(no Cancer)P(Positive if no Cancer) + P(Cancer)P(Positive if Cancer))`

=
`((0.0263)(0.9989))/((1 - 0.0263)(0.0866) + (0.0263)(0.9989))`

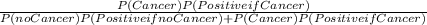
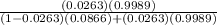
= 0.2375