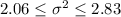Question

The widths of 79 randomly selected window blinds were found to have a standard deviation of 2.37. Construct the 95% confidence interval for the population standard deviation of the widths of all window blinds in this factory. Round your answers to two decimal places.

Answer 1

`((78)(2.37)^2)/(104.316) \leq \sigma^2 \leq ((78)(2.37)^2)/(55.466)`

`4.254 \leq \sigma^2 \leq 8.000`

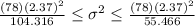
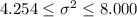
And for the deviation we just need to take the square root of the variance and we got:

`2.06 \leq \sigma^2 \leq 2.83`

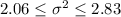
Explanation:

Data given and notation

s=2.37 represent the sample standard deviation

`\bar x` represent the sample mean

n=79 the sample size

Confidence=95% or 0.95

A confidence interval is "a range of values that’s likely to include a population value with a certain degree of confidence. It is often expressed a % whereby a population mean or variance lies between an upper and lower interval".

The margin of error is the range of values below and above the sample statistic in a confidence interval.

The Chi square distribution is the distribution of the sum of squared standard normal deviates .

Calculating the confidence interval

The confidence interval for the population variance is given by the following formula:

`((n-1)s^2)/(\chi^2_(\alpha/2)) \leq \sigma^2 \leq ((n-1)s^2)/(\chi^2_(1-\alpha/2))`

The next step would be calculate the critical values. First we need to calculate the degrees of freedom given by:

`df=n-1=79-1=78`

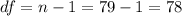
Since the Confidence is 0.95 or 95%, the value of
`\alpha=0.05` and
`\alpha/2 =0.025`, and we can use excel, a calculator or a table to find the critical values.

The excel commands would be: "=CHISQ.INV(0.025,78)" "=CHISQ.INV(0.975,78)". so for this case the critical values are:

`\chi^2_(\alpha/2)=104.316`

`\chi^2_(1- \alpha/2)=55.466`

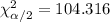
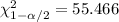
And replacing into the formula for the interval we got:

`((78)(2.37)^2)/(104.316) \leq \sigma^2 \leq ((78)(2.37)^2)/(55.466)`

`4.254 \leq \sigma^2 \leq 8.000`

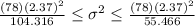
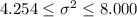
And for the deviation we just need to take the square root of the variance and we got:

`2.06 \leq \sigma^2 \leq 2.83`