Answer:
Total probability is 0.1608
Explanation:
The Binomial Probability expression is:
∑(r=0 to n)
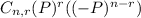
where
n = number of attempts
r = successes
P = Probability of each success and
-P = Probability of each Failure
We will sum all the the attempts to achieve the sum of 1 but
For this problem, we are looking for only one condition which is - playing the game five time and winning twice so P =
 and -P =
and -P =

So, our final solution is
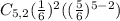 = 0.1608 = 16.08%
= 0.1608 = 16.08%