Question

Assume that the weights of quarters are normally distributed with a mean of 5.67 g and a standard deviation 0.070 g. A vending machine will only accept coins weighing between 5.48 g and 5.82 g. What percentage of legal quarters will be rejected?

Answer 1

The percentage of legal quarters that will be rejected is 1.954 %.

Step-by-step explanation:

Here we are required to find

P(X<5.48 or X>5.82)

We have μ = 5.67 and σ = 0.07 where the range is between 5.48 and 5.82 we each z-score given by

`z =(x-\mu)/(\sigma)`

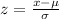
Therefore for 5.48 we have
`z_(5.48) = (5.48 -5.67)/(0.07)` = -2.714

and for 5.82 we have
`z_(5.82) = (5.82 -5.67)/(0.07)` = 2.143

Therefore we have the area of interest on the normal distribution chart given by

P(Z<-2.714) + P(Z > 2.143) = P(Z<-2.714) + (1 - P(Z < 2.143))

+ 0.00336 + 1 - 0.98382 = 0.01954

= 0.01954 × 100 = 1.954 %

Therefore 1.954 percentage of legal quarters will be rejected.