Answer:
(a) Test statistic (t) for the hypothesis test is -5.0498
(b) Null hypothesis is rejected .
Explanation:
We are given that a psychologist has developed an aptitude test which consists of a series of mathematical and vocabulary problems. They want to test the hypothesis that the mean test score is 80, i.e.;
Null Hypothesis,
 :
:
 = 80
= 80
Alternate Hypothesis,
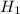 :
:
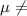 80
80
We are given the sample data of 40 people, i.e. n = 40 ;
Sample mean, X bar =
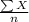 =
=
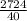 = 68.1
= 68.1
Sample standard deviation, s =
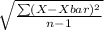 = 14.904
= 14.904
The test statistics we will use here is;
T.S. =
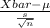 ~
~
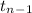
=
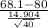 ~
~
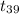
= -5.0498
So, test statistic (t) for the hypothesis test is -5.0498 .
(b) Now, at level of significance of 0.05, t table gives critical value of between [-2.0225 , 2.0225] . Since our test statistics does not lie in the range of critical value means it lies in the rejection region so we have sufficient evidence to reject null Hypothesis.
Therefore, null hypothesis is rejected .