Question

The number of surface flaws in plastic panels used in the interior of automobiles has a Poisson distribution with a mean of 0.05 flaw per square foot of plastic panel. Assume that an automobile interior contains 10 square feet of plastic panel.(a) What is the probability that there are no surface flaws in an auto's interior?(b) If 10 cars are sold to a rental company, what is the probability that none of the 10 cars has any surface flaws?

Answer 1

(a) Probability that there are no surface flaws in an auto's interior is 0.6065 .

(b) If 10 cars are sold to a rental company, what is the probability that none of the 10 cars has any surface flaws is 0.00673 .

Explanation:

We are given that the number of surface flaws in plastic panels used in the interior of automobiles has a Poisson distribution with a mean of 0.05 flaws per square foot of plastic panel.

Let X = Distribution of number of surface flaws in plastic panels

So, X ~ Poisson(
`\lambda`)

The mean of Poisson distribution is given by, E(X) =
`\lambda` = 0.05

which means, X ~ Poisson(0.05)

The probability distribution function of a Poisson random variable is:

`P(X=x)=(e^(-\lambda)\lambda^(x))/(x!); for x=0,1,2,3...`

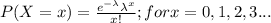
Now, we know that
`\lambda` for per square foot of plastic panel is 0.05 and we are given that an automobile interior contains 10 square feet of plastic panel.

Therefore, for 10 square foot of plastic panel is = 10 * 0.05 = 0.5

(a) Probability that there are no surface flaws in an auto's interior =P(X=0)

P(X = 0) =
`(e^(-0.5)*0.5^(0))/(0!)` =
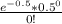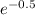`e^(-0.5)` = 0.6065

(b) If 10 cars are sold to a rental company, what is the probability that none of the 10 cars has any surface flaws =
`P(X = 0)^(10)`

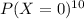
So,
`P(X = 0)^(10)` =
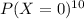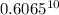`0.6065^(10)` = 0.00673