Question

Soil that contains 30% clay is added to soil that contains 70% clay to create 10 gallons of soil containing 50% clay. How much of each of the soils was combined?

Answer 1

5 gallons of soil that contains 30% clay and 5 gallons of soil that contains 70% clay is combined

Explanation:

Given:

Soil that contains 30% clay is added to soil that contains 70% clay to create 10 gallons of soil containing 50% clay.

Now, to find the quantity of each of the soils was combined.

Total quantity of soil containing 50% clay = 10 gallons.

Let the quantity of soil that contains 30% clay be
`x.`

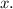
And let the quantity of soil that contains 70% clay be
`10-x.`

Now, to get the quantity of soils:

`30\%\ of\ x+70\%\ of\ (10-x)=50\%\ of\ 10`

`(30)/(100) * x+(70)/(100) * (10-x)=(50)/(100) * 10`

`0.30x+0.70(10-x)=5`

`0.30x+7-0.7x=5`

`7-0.4x=5`

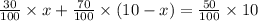
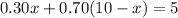
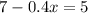
Subtracting both sides by 7 we get:

`-0.4x=-2`

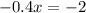
Dividing both sides by -0.4 we get:

`x=5.`

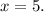
The quantity of soil that contains 30% clay = 5 gallons.

Now, substituting the value of
`x` we get:

`10-x\\\\=10-5\\\\=5.`

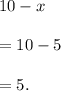
The quantity of soil that contains 70% clay = 5 gallons.

Therefore, 5 gallons of soil that contains 30% clay and 5 gallons of soil that contains 70% clay is combined.