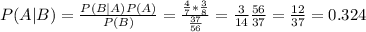Question

Box 1 contains 3 blue and 5 red balls, whereas Box 2 contains 2 blue and 4 red ball. A ball is randomly chosen from Box 1 and then transferred to Box 2, and a ball is then randomly selected from Box 2. What is the conditional probability that the transferred ball was blue, given that a red ball is selected from Box 2 (round off to second decimal place)?

Answer 1

0.32

Explanation:

Let A be the event that the transferred ball was blue.

B be the event that the red ball is selected from box 2

C be the event that the transferred ball was red

Then:

P(A) be the probability that the transferred ball was blue, which is 3/8

P(C) be the probability that the transferred ball was red, which is 5/8

P(B|A) is the probability that selected ball is red, given that the transferred ball was blue, which is 4/7

P(B|C) is the probability that selected ball is red, given that the transferred ball was red, which is 5/7

P(B) is the probability that the selected ball is red, which there are 2 scenarios, given that the transferred ball is blue and red

P(B) = P(B|A)P(A) + P(B|C)P(C)

`P(B) = (4)/(7)(3)/(8) + (5)/(7)(5)/(8)`

`P(B) = (3)/(14) + (25)/(56) = (37)/(56)`

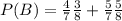
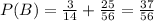
P(A|B) is the probability that the transferred ball was blue, given that a red ball is selected from Box 2, which can be solved using Bayes theorem

`P(A|B) = (P(B|A)P(A))/(P(B)) = ((4)/(7)*(3)/(8))/((37)/(56)) = (3)/(14)(56)/(37) = (12)/(37) = 0.324`