Question

An inductor is connected to the terminals of a battery that has an emf of 12.0 V and negligible internal resistance. The current is 4.86 mA at 0.725 ms after the connection is completed. After a long time, the current is 6.45 mA.

(a) What is the resistance R of the inductor?
(b) What is the inductance L of the inductor?

Answer 1

(a) 1860 Ω

(b) 0.16H

Step-by-step explanation:

This is an RL circuit as it contains an inductor with and inherent resistance.

The current, I, flowing through such circuit is given by;

I =
`(E)/(R)`[1 -
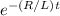`e^(-(R/L)t)`] --------------(i)

Where;

E = emf of the circuit = 12.0V

R = Resistance of the inductor

L = inductance of the inductor

t = time taken for the flow of current

(a) After a long time, i.e t → ∞, the current becomes saturated (i.e maximum) and the value is 6.45mA.

At this time,
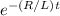`e^(-(R/L)t)` (from equation (i)) becomes 0 and current I, becomes;

I =
`(E)/(R)` -------------------(ii)

Now substitute the value of E and I into equation (ii) as follows;

6.45 x 10⁻³=
`(12.0)/(R)`

R =
`(12.0)/(6.45 * 10^(-3))`

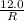
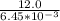
R = 1860Ω

Therefore, the resistance of the inductor is 1860 Ω

(b) To get the inductance L of the inductor, we substitute I = 4.86mA at time t = 0.725ms into equation (i) as follows;

4.86 x 10⁻³ =
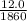`(12.0)/(1860)`[1 -
`e^(-(1860/L)0.00486)`]

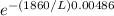4.86 x 10⁻³ x 1860 = 12.0[1 -
`e^(-(1860/L)0.00486)`]

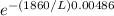0.7533 = [1 -
`e^(-(1860/L)0.00486)`]

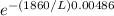1 - 0.7533 =
`e^(-(1860/L)0.00486)`

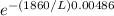
0.2467 =
`e^(-(1860/L)0.00486)`

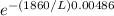
Take the natural log of both sides

ln(0.2467) = -1860 x 0.00468 / L

-1.3996 = -8.7048 / L

L = -1.3996 / -8.7048

L = 0.16H

Therefore, the inductance of the inductor is 0.16H

Answer 2

R = 2481 Ω

L= 1.67 H

Step-by-step explanation:

(a) We have an inductor L which has an internal resistance of R. The inductor is connected to a battery with an emf of E = 12.0 V. So this circuit is equivalent to a simple RL circuit. It is given that the current is 4.86 mA at 0.725 ms after the connection is completed and is 6.45 mA after a long time. First we need to find the resistance of the inductor. The current flowing in an RL circuit is given by

i = E/R(1 -e^(-R/L)*t) (1)

at t --> ∞ the current is the maximum, that is,

i_max = E/R

solve for R and substitute to get,

R= E/i_max

R = 2481 Ω

(b) To find the inductance we will use i(t = 0.940 ms) = 4.86 mA, solve (1) for L as,

Rt/L = - In (1 - i/i_max )

Or,

L = - Rt/In (1 - i/i_max )

substitute with the givens to get,

L = -(2481 Si) (9.40 x 10-4 s)/ In (1 - 4.86/6.45 )

L= 1.67 H

note :

error maybe in calculation but method is correct