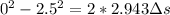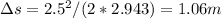Question

Two football players are pushing a 60 kg blocking sled across the field at a constant speed of 2.5 m/s. The coefficient of kinetic friction between the grass and the sled is 0.30. Once they stop pushing, how far will the sled slide before coming to rest

Answer 1

Once they stop pushing, the sled will slide 0.53m before coming to rest. The calculation can be found below in the attachment.

Step-by-step explanation:

This problem involves energy concepts and the law of conservation is needed foe an easy solution. The energy conservation equation is used in this solution which is

K1 + U1 + Wf = K2 + U2

Where K1 and K2 are the initial and final kinetic energies and similarly U1 and U2 the initial and final potential energies. Wf is the workdone due to friction.

The initial and final potential energies are zero. The final kinetic energy is also zero.

Given v = 2.5m/s

Coefficient of friction = 0.3 see attachment below.

Answer 2

1.06 m

Step-by-step explanation:

The kinetic friction of the grass on the sled is the product of friction coefficient and the normal force, which equals to gravitational force. Let g = 9.81 m/s2:

`F_f = \mu N = \mu mg = 0.3*60*9.81 = 176.58 N`

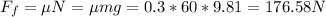
So the deceleration caused by kinetic friction on the 60 kg sled is

`a = F_f / m = 176.68 / 60 = 2.943 m/s^2`

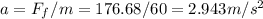
If the sled on a speed of 2.5m/s and then subjected to a deceleration of 2.943 m/s2, then we can use the following equation of motion to find out the distance traveled by the sled before rest:

`v^2 - v_0^2 = 2a\Delta s`

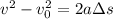
where v = 0 m/s is the final velocity of the sled when it stops,
`v_0` = 2.5m/s is the initial velocity of the can when it hits, a = -2.943 m/s2 is the deceleration, and
`\Delta s` is the distance traveled, which we care looking for:

`0^2 - 2.5^2 = 2*2.943\Delta s`

`\Delta s = 2.5^2 / (2*2.943) = 1.06 m`