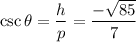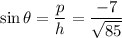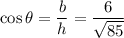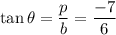Question

Suppose 0 is an angle in the standard position whose terminal side is in Quadrant IV and cot0= -6/7 Find the exact values of the five remaining trigonometric functions of 0

Answer 1

`\sin \theta=(p)/(h) =(-7)/(√(85) )`,
`\cos \theta=(b)/(h) =(6)/(√(85))`,
`\tan \theta=(p)/(b) =(-7)/(6)`,

`\sec \theta=(h)/(b) =(√(85) )/(6)` and
`\csc \theta=(h)/(p) =(-√(85))/( 7)`

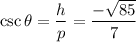
Step-by-step explanation:

Given,

`\cot \theta= (-6)/(7)`

To find, the exact values of the five remaining trigonometric functions of
`\theta` = ?

We know that,

`\cot \theta= (-6)/(7)=(b)/(p)`

Where, b = base and p = perpendicular

By Pythagoras's theorem,

Hypotaneous,
`h=√(p^2+b^2)`

`=√((-6)^2+7^2)=√(36+49) =√(85)`

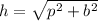
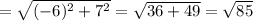
In IVth quadrant,

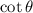`\cot \theta` and
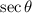`\sec \theta` are positive.

`\sin \theta=(p)/(h) =(-7)/(√(85) )`,
`\cos \theta=(b)/(h) =(6)/(√(85))`,
`\tan \theta=(p)/(b) =(-7)/(6)`,

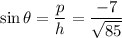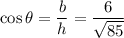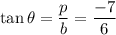`\sec \theta=(h)/(b) =(√(85) )/(6)` and
`\csc \theta=(h)/(p) =(-√(85))/( 7)`