Question

The population of a town grows at a rate proportional to the population present at time t. The initial population of 500 increases by 25% in 10 years. What will be the population in 40 years

Answer 1

The population in 40 years will be 1220.

Explanation:

The population of a town grows at a rate proportional to the population present at time t.

This means that:

`P(t) = P(0)e^(rt)`

In which P(t) is the population after t years, P(0) is the initial population and r is the growth rate.

The initial population of 500 increases by 25% in 10 years.

This means that
`P(0) = 500, P(10) = 1.25*500 = 625`

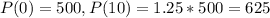
We apply this to the equation and find t.

`P(t) = P(0)e^(rt)`

`625 = 500e^(10r)`

`e^(10r) = (625)/(500)`

`e^(10r) = 1.25`

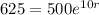
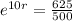
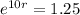
Applying ln to both sides

`\ln{e^(10r)} = ln(1.25)`

`10r = ln(1.25)`

`r = (ln(1.25))/(10)`

`r = 0.0223`

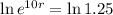
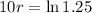
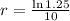
So

`P(t) = 500e^(0.0223t)`

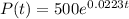
What will be the population in 40 years

This is P(40).

`P(t) = 500e^(0.0223t)`

`P(40) = 500e^(0.0223*40) = 1220`

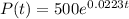
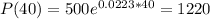
The population in 40 years will be 1220.