Question

Each of Alice, Bob, and Chuck shoots at a target once, and hits it independently with probabilities 1/6, 1/4, and 1/3, respectively. If only one shot hit the target, what is the probability that Alice's shot hit the target?

Answer 1

0.1935 or 19.35%

Explanation:

If only one shot hit the target, two other people missed the target. The probability that only one person hit the target is:

`P(X=1) =P(Only\ A)+P(Only\ B)+P(Only\ C)\\P(X=1) =(1)/(6)*(3)/(4)* (2)/(3) +(5)/(6)*(1)/(4)* (2)/(3) +(5)/(6)*(3)/(4)* (1)/(3) \\P(X=1) = 0.4306`

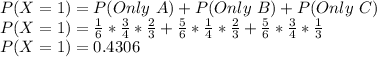
The probability that only Alice hit the shot is:

`P(Only\ A)=(1)/(6)*(3)/(4)* (2)/(3)\\P(Only\ A) = 0.08333`

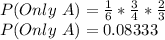
Therefore, the probability that Alice's shot hit the target, given that only one shot hit the target:

`P(Only\ A|X=1) = (P(Only\ A))/(P(X=1)) \\P(Only\ A|X=1) =(0.08333)/(0.4306)\\P(Only\ A|X=1) =0.1935=19.35\%`

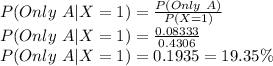
The probability is 0.1935 or 19.35%.