Question

If the initial upward speed of the ball in Activity 7 C.2 is 10m/s, and the ball is releasedat a height of 1.5 m above the oor, what isthe maximum height above the oorthat theball reaches? How farabove Christine's handis the ball when it reaches its maximumheight, and how is this value related to your answer to 4 in Activity 7 C.2?

Answer 1

6.602m above the floor

5.102m above christine's hand.

Step-by-step explanation:

This problem involves the concept of motion under free fall.

At maximum height the velocity is 0m/s

V = u -gt

u = 10m/s and g =9.8m/s²

t is the time taken to reach maximum height and is unknown.

On substitution

0 = 10 - 9.8t

9.8t = 10

t = 10 / 9.8

t = 1.02s

H = h + ut -1/2gt²

H is the height

h is the initial height = 1.5m

H = 1.5 + 10×1.02 - 1/2 ×9.8×1.02² = 6.602m

The distance the ball travels above christine's hand is 6.602 - 1.50m = 5.502m

Answer 2

6.5 m above the floor and 5 m above Christine's hand when it reaches the maximum height.

Step-by-step explanation:

Let g = 10 m/s2 be the gravitational deceleration that affects the ball vertical motion so it comes to the maximum height at 0 speed. We can use the following equation of motion to find out the distance traveled by the ball from where it's thrown:

`v^2 - v_0^2 = 2g\Delta s`

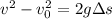
where v = 0 m/s is the final velocity of the ball when it reaches maximum level,
`v_0` = 10m/s is the initial velocity of the ball when it starts, g = -10 m/s2 is the deceleration, and
`\Delta s` is the distance traveled, which we care looking for:

`0^2 - 10^2 = -2*(-10)\Delta s`

`\Delta s = 100 / (2 * 10) = 5 m`

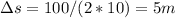
So the ball is 5 m above Christine' hands when it reaches maximum height, and since the hand is 1.5 m above the floor, the ball is 5 + 1.5 = 6.5 m above the floor when it reaches maximum height.