Answer:

Explanation:
we know that
If line I s a perpendicular bisector of line segment R Q at point T
then
T is the midpoint of line segment RQ
and

we have
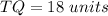
so

Find the value of x
we have
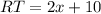
substitute the value of RT
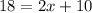
solve for x
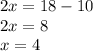
Find the value of SQ
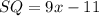
substitute the value of x
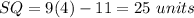
we have that
Triangle RTS and Triangle QTS are congruent by SAS
see the attached figure to better understand the problem
so

therefore
