Question

A 58.0 kg person is riding in a car moving at 23.0 m/s when the car runs into a bridge abutment. (Assume the initial velocity is in the positive direction.) (a) Calculate the average force (in N) on the person if he is stopped by a padded dashboard that compresses an average of 1.00 cm. (Indicate the direction with the sign of your answer.)

Answer 1

1534100 N in the opposite direction of his initial velocity

Step-by-step explanation:

1 cm = 0.01 m

So the person is subjected to a deceleration that stops his initial motion of 23 m/s within a distance of 0.01 m. We can use the following equation of motion to find out the deceleration:

`v^2 - v_0^2 = 2a\Delta s`

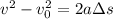
where v = 0 m/s is the final velocity of the person,
`v_0` = 23m/s is the initial velocity of the person when hit, a is the deceleration, and
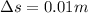`\Delta s = 0.01 m` is the distance traveled:

`0^2 - 23^2 = 2*a*0.01`

`a = -23^2 / (2*0.01) = -26450 m/s^2`

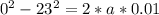
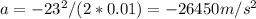
We can calculate the average force he's subjected to using Newton's2nd law:

`F = am = -26450 * 58 = -1534100 N`

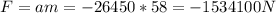
So he is subjected to a force of 1534100 N in the opposite direction of his initial velocity.