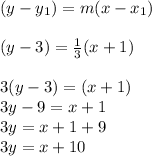Answer:
Equation of the line:
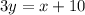
Explanation:
If an equation of a line is perpendicular, its gradient will be such that:
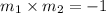
Since the gradient /slope of the given equation can be inferred as -3, the gradient of the perpendicular line will be
 .
.
Coordinates of a point on the line are (3,-1)