A solid lies between planes perpendicular to the x-axis at x = -11 and x = 11. The cross-sections perpendicular to the x-axis between these planes are squares whose bases run from the semicircle y equals negative
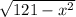
to the semicircle y equals
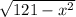
. Find the volume of the solid.