Question

Does the point (1, StartRoot 7 EndRoot) lie on the circle shown? Explain. Yes, the distance from (–2, 4) to (–2, 0) is 4 units. Yes, the distance from (–2, 0) to (1, StartRoot 7 EndRoot) is 4 units. No, the distance from (–2, 0) to (1, StartRoot 7 EndRoot) is not 4 units. No, the distance from (–2, 4) to (1, StartRoot 7 EndRoot) is not 4 units.

Answer 1

Answer: B

Explanation:

Answer 2

Yes, the distance from
`(-2,0)\ to\ (1,√(7))\ is\ 4\ units`

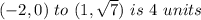
Explanation:

The picture of the question in the attached figure

step 1

Find the equation of the circle

we know that

The equation of the circle is equal to

`(x-h)^(2)+(y-k)^(2) =r^(2)`

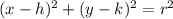
where

(h,k) is the center

r is the radius

In this problem we have

`(h,k)=(-2,0)`

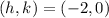
and the radius is equal to the distance between the center and the point (-2,4)

so

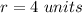`r=4\ units` ----> look at the graph

substitute in the equation

`(x+2)^(2)+(y)^(2) =4^(2)\\(x+2)^(2)+(y)^(2) =16`

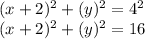
step 2

If the distance between the center and the point is equal to the radius of the circle , then the point lie on the circle

the formula to calculate the distance between two points is equal to

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}\\A(-2,0)\\B(1,√(7))`

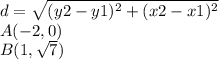
substitute the values

`d=\sqrt{(√(7)-0)^(2)+(1+2)^(2)}\\d=√(7+9)\\d=\sqrt16}=4\ units`

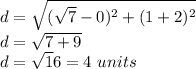
therefore

the point lie on the circle