Question

two drain pipes, working together, can drain a tank in 4 hours. Working alone, it would take the smaller pipe 6 hours longer than it would take the larger pipe to drain the tank. How long would it take the smaller pipe alone to drain the tank.

Answer 1

12 hours

Explanation:

Let the larger pipe can drain the tank in x hours

Than, time taken by smaller tank to drain the tank= (x+6) hours

If working togather, both pipe can drain the tank= 4 hours

A.T.Q

`(1)/(x)` +
`(1)/(x+6)`=
`(1)/(4)`

`(x+x+6)/(x(x+6))`=
`(1)/(4)`

`(2x+6)/(x^(2)+6x )`=
`(1)/(4)`

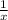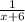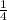
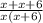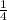
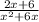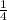
8 x +24=
`x^(2)` + 6 x

`x^(2)` - 2 x- 24= 0

`x^(2)` -6 x+ 4 x -24=0

x(x-6) + 4(x-6)= 0

(x-6)(x+4)=0

X= 6, X=-4 is rejected

Hence, time taken by larger tank to fill the drain= 6 hours

Hence, time taken by smaller tank to drain the tank = 6+6= 12 hours

Hence, the correct answer is 12 hours