Answer:
-186,450
Explanation:
Sum of arithmetic series formula
![S_n=(n)/(2)[2a+(n-1)d]](https://img.qammunity.org/2023/formulas/mathematics/high-school/3xswszu9aa97ib3vxzethlaa34iy1xjgl7.png)
where:
- a is the first term
- d is the common difference between the terms
- n is the total number of terms in the sequence
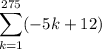
To find the first term, substitute
 into
into
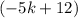
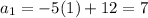
To find the common difference, find
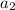 then subtract
then subtract
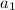 from
from
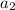 :
:
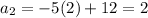
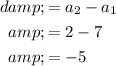
Given:
![\begin{aligned}S_(275) & = (275)/(2)[2(7)+(275-1)(-5)]\\& = (275)/(2)[14-1370]\\& = (275)/(2)[-1356]\\& = -186450\end{aligned}](https://img.qammunity.org/2023/formulas/mathematics/high-school/nnvs2f38mbslr57sxcqt6wd6gq4v6rnnl6.png)