Question

A student takes an exam containing 1818 true or false questions. If the student guesses, what is the probability that he will get exactly 66 questions right? Round your answer to four decimal places.

Answer 1

Probability

p=66×100/1818=3.6303630363%

After rounding to 4 decimals:

p=3.6304%

Answer 2

0.0708 = 7.08% probability that he will get exactly 6 questions right.

Explanation:

For each question, there are only two possible outcomes. Either the student guesses the correct answer, or he guesses the wrong answer. The probability of guessing the correct answer in a question is independent from other questions. So we use the binomial probability distribution to solve this question.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

In which
`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

And p is the probability of X happening.

18 questions

This means that
`n = 18`

True or false, guessed.

Each question has two possible answers, so
`p = (1)/(2) = 0.5`

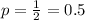
If the student guesses, what is the probability that he will get exactly 6 questions right?

This is
`P(X = 6)`

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 6) = C_(18,6).(0.5)^(6).(0.5)^(12) = 0.0708`

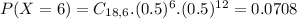
0.0708 = 7.08% probability that he will get exactly 6 questions right.