When we multiply two functions, the degree is the sum of the original degrees. So, since the degree of the product is 2, we have two cases:
- One of the function has already degree 2, and the other is constant (degree 0)
- Both functions are linear.
The first case is actually impossible, because otherwise the sum would have degree 2 as well. So, we know that both
 and
and
 are linear. In other words, we have
are linear. In other words, we have

for some
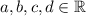
We know that the sum is
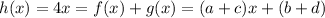
we deduce that

So, we know that:
- Both functions must be quadratic. FALSE, otherwise the product would have degree 4;
- Both functions must have a constant rate of change. TRUE, linear functions have a constant rate of change;
- Both functions must have a y-intercept of 0. FALSE, it is only required that the sum of the y-intercepts is 0, they don't have to be both zero;
- The rate of change of f(x) and g(x) must be opposites. FALSE, their sum must be 4;
- The y-intercepts of f(x) and g(x) must be opposites. TRUE, their sum must be zero.