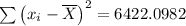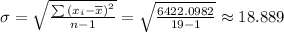Question

In Applied Life Data Analysis (Wiley, 1982), Wayne Nelson presents the breakdown time of an insulating fluid between electrodes at 34 kV. The times, in minutes, are as follows: 0.15, 0.82, 0.81, 1.44, 2.70, 3.28, 4.00, 4.70, 4.96, 6.49, 7.25, 8.03, 8.40, 12.15, 31.89, 32.47, 33.79, 36.80, and 72.92. Calculate the sample mean and sample standard deviation. Round the answers to 3 decimal places.

Answer 1

The sample mean is
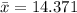`\bar{x}=14.371` min.

The sample standard deviation is
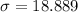`\sigma = 18.889` min.

Explanation:

We have the following data set:

`\begin{array}{cccccccc}0.15&0.82&0.81&1.44&2.70&3.28&4.00&4.70\\4.96&6.49&7.25&8.03&8.40&12.15&31.89&32.47\\33.79&36.80&72.92&&&&&\end{array}`

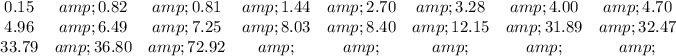
The mean of a data set is commonly known as the average. You find the mean by taking the sum of all the data values and dividing that sum by the total number of data values.

The formula for the mean of a sample is

`\bar{x} = \frac{{\sum}x}{n}`

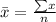
where,
`n` is the number of values in the data set.

`\bar{x}=(0.15+0.82+0.81+1.44+2.7+3.28+4+4.7+4.96+6.49+7.25+8.03+8.4+12.15+31.89+32.47+33.79+36.80+72.92)/(19)\\\\\bar{x}=14.371`

The standard deviation measures how close the set of data is to the mean value of the data set. If data set have high standard deviation than the values are spread out very much. If data set have small standard deviation the data points are very close to the mean.

To find standard deviation we use the following formula

`\sigma = \sqrt{ \frac{ \sum{\left(x_i - \overline{x}\right)^2 }}{n-1} }`

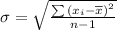
The mean of a sample is
`\bar{x}=14.371`.

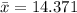Create the below table.

Find the sum of numbers in the last column to get.

`\sum{\left(x_i - \overline{X}\right)^2} = 6422.0982`

`\sigma = \sqrt{ \frac{ \sum{\left(x_i - \overline{x}\right)^2 }}{n-1} } = \sqrt{ ( 6422.0982 )/( 19 - 1) } \approx 18.889`