The clouds are 226.68 meters above the spotlight.
Explanation:
Step 1:
The angle measuring device is 65 meters from the spotlight and the angle of elevation from the ground to the spot of light is 74°.
So a right-angled triangle can be formed using these measurements. The angle of the triangle is 74° while the opposite side of the triangle measures x meters while the adjacent side of the triangle measures 65 meters.
We need to calculate the opposites side's length of the triangle.
Step 2:
Since we have the adjacent side's length and need to calculate the opposite side's length we use the tan of the given angle.
The opposite side of the triangle = x meters.
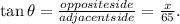
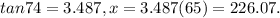
So the spot of light is 226.07 meters above from the spotlight.