Answer:
15 units
Explanation:
In the image attached you can notice that line ZY is tangent at point Y.
Remember that the radius is always perpendicular to tangents, by definition, that means
 .
.
That means
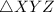 is a right triangle where
is a right triangle where
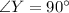 .
.
All these facts are deducted form having ZY as a tangent.
We know by given that
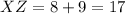
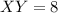 , becaus it's the radius.
, becaus it's the radius.
Using Pythagorean Theorem
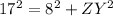
Solving for
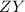
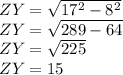
Therefore, the length of ZY must be 15 units to be tangent to circle X.