Question

You have just received notification that you have won the $2.06 million first prize in the Centennial Lottery. However, the prize will be awarded on your 100th birthday (assuming you’re around to collect), 74 years from now. What is the present value of your windfall if the appropriate discount rate is 10 percent? (Enter your answer in dollars, not millions, e.g., 1,234,567. Do not round intermediate calculations and round your answer to 2 decimal places, e.g., 32.16.) Present value $

Answer 1

$1781.59

Step-by-step explanation:

The present value is the current value of a future income or stream of money, at a specified interest rate (or discount rate).

The future value is the value of an income at a future date based on a rate of interest or discount rate.

We will use the present value (and future value) formula here to solve this problem. The formula is:

`PV=(FV)/((1+r)^n)`

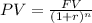
Where

PV is the present value

FV is the future value

r is the rate of interest (or discount rate)

n is the time in years

Given in the problem, something that you will win 74 years from now, it will be worth $2.06 million, so this is the future value.

FV = 2,060,000

The rate of interest (discount rate) is 10 percent, which means:

r = 10% = 10/100 = 0.1

The time period in years would be 74 years, because 74 years from now you will get the money, so:

n = 74

Now, we plug these into the equation and get our answer:

`PV=(FV)/((1+r)^n)\\PV=(2060000)/((1+0.1)^(74))\\PV=(2060000)/(1.1^(74))\\PV=1781.59`

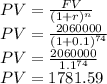
Hence the present value is $1781.59