Answer:
- The expected payoff for option B is $100.
Step-by-step explanation:
The payoff is a random variable. The expected value, E(X), of a random variable is determined as the sum of the products of the value of each outcome by its corresponding probability:
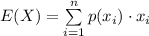
For option B:
- number of outcomes, n = 2 (head and tail)
- value of x₁ = head: 0
- probability of head, p(x₁) = 0.5
- value of x₂ = tail: $200
- parobablity of tail, p(x₂) = 0.5
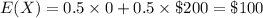
Hence, the expected pay off is $100.