Question

5.According to the Bureau of Labor Statistics, in calendar year 2000, the average duration of unemployment was 12.7 weeks, with a standard deviation of 0.3 weeks. Assuming that distribution is approximately normal, what is the probability that a randomly selected individual who was unemployed in 2000 would have been unemployed between 12 and 13 weeks?

Answer 1

Probability that a randomly selected individual who was unemployed in 2000 would have been unemployed between 12 and 13 weeks is 0.83144 .

Explanation:

We are given that according to the Bureau of Labor Statistics, in calendar year 2000, the average duration of unemployment was 12.7 weeks, with a standard deviation of 0.3 weeks.

Let X = randomly selected individual who was unemployed in 2000

Since distribution is approximately normal, so X ~ N(
`\mu=12.7,\sigma^(2) = 0.3^(2)`)

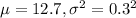The z score probability distribution is given by;

Z =
`(X-\mu)/(\sigma)` ~ N(0,1)

where,
`\mu` = population mean = 12.7 weeks

`\sigma` = population standard deviation = 0.3 weeks

So, the probability that a randomly selected individual who was unemployed in 2000 would have been unemployed between 12 and 13 weeks is given by = P(12 < X < 13) = P(X < 13) - P(X <= 12)

P(X < 13) = P(
`(X-\mu)/(\sigma)` <
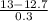`(13-12.7)/(0.3)` ) = P(Z < 1) = 0.84134

P(X <= 12) = P(
`(X-\mu)/(\sigma)` <
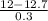`(12-12.7)/(0.3)` ) = P(Z < -2.33) = 1 - P(Z <= 2.33) = 1 - 0.99010

= 0.0099

Therefore, P(12 < X < 13) = 0.84134 - 0.0099 = 0.83144 .