Answer:
Yes at the level of 0.02 significance
Explanation:
we want to compare if P₁ = P₂
P1 = 9/142= 0.0634
P2 = 5/268 = 0.0187
P = 14/410 = 0.03414
significance level, α = 0.02
Test statistic, z =
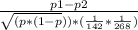
Test Statistic, z =
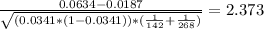
Test statistic, z = 2.373
p-value = 2*p(z<|z₀|) = 2*p(z<2.37) = 0 .0176
Answer: Since p-value (0.0176) is less than the significance level, α (0.02), the null hypothesis can not hold. we can therefore say that at 0.02 level of significance, there is sufficient evidence, statistically, that p₁ is different from p₂