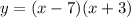Question

What is the equation of the quadratic function with a vertex at (2,-25) and an x-intercept at(7,0)

Answer 1

the answer is d

Step-by-step explanation:

Answer 2

The equation of the quadratic function is
`y=(x-7)(x+3)`

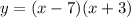
Step-by-step explanation:

The vertex form of the quadratic function is given by

`y=a(x-h)^(2)+k`

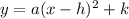
It is given that the quadratic function has a vertex at
`(2,-25)`

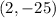
The vertex is represented by the coordinate
`(h,k)`

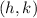
Hence, substituting
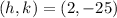`(h,k)=(2,-25)` in the vertex form, we get,

`y=a(x-2)^(2)-25`

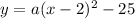
Now, substituting the x - intercept
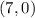`(7,0)` , we have,

`0=a(7-2)^(2)-25`

`0=a(5)^(2)-25`

`25=a(25)`

`1=a`

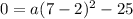
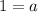
Thus, the value of a is 1.

Hence, substituting
`a=1`,
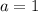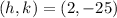`(h,k)=(2,-25)` in the vertex form
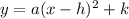`y=a(x-h)^(2)+k` , we get,

`y=1(x-2)^(2)-25`

`y=(x-2)^(2)-25`

`y=x^2-2x+4-25`

`y=x^2-2x-21`

`y=(x-7)(x+3)`

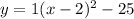
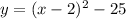
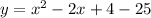
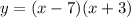
Thus, the equation of the quadratic function is
`y=(x-7)(x+3)`