Answer:
The probability of event A is 0.2160.
The probability of event B is 0.2153.
Explanation:
Assume that the random variable X is defined as the number of defective components in a lot.
It is provided that of the 1060 component 229 are defective.
The probability of selecting a defective component is:
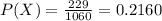
The proportion of defective components in a lot of 1060 is 0.2160.
It is provided that two components are selected to be tested.
Assuming the selection were without replacement.
A = the first component drawn is defective
B = the second component drawn is defective
- Compute the probability of event A:
The probability of selecting a defective component from the entire lot
of 1060 component is 0.2160.
Thus, the probability of event A is 0.2160.
- Compute the probability of event B:
According to event A, the first component selected was defective.
So now there are 228 defective components among 1059
components.
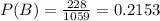
Thus, the probability of event B is 0.2153.
Both the probabilities are almost same.
This implies that the probability of selecting a defective component from the entire population of these components is approximately 0.2160.