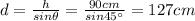Question

A block with mass m = 4.90 kg is placed against a spring on a frictionless incline with angle θ = 45° (The block is not attached to the spring). The spring, with spring constant k = 35.0 N/cm, is compressed 16.0 cm and then released.a.) What is the elastic potential energy of the compressed spring?b.) What is the change inn the gravitational potential energy of the block-Earth system as the block moves from the release point to its highest point on the incline?c.) How far along the inline is the highest point from the release point?

Answer 1

a) 44.8J

b) 44.8J

c) 127cm

Step-by-step explanation:

a) The elastic potential energy of a compressed spring is given by the formula:

`U_e=(1)/(2) kx^(2)`

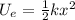
Where U_e is the elastic potential energy, k is the spring constant and x is the distance the spring is compressed. In this case, we have:

`U_e=(1)/(2) (35.0N/cm)(16.0cm)^(2) = 4480Ncm`

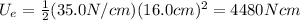
To express the result in Joules, we have to use the fact that 1cm=0.01m. Then:

`U_e=4480Ncm=4480N(0.01m)=44.8J`

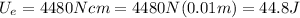
In words, the elastic potential energy of the compressed spring is 44.8J.

b) Using the law of conservation of mechanical energy, we have that:

`E_o=E_f\\\\U_(eo)+U_(go)+K_o=U_(ef)+U_(gf)+K_f`

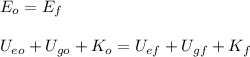
Taking t=0 the moment in which the block is released, and t=t_f the point of its maximum height, we have that
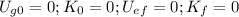`U_(g0)=0;K_0=0;U_(ef)=0;K_f=0` because in t=0 the block has no speed and is in tis lowest point; and in t=t_f the block has stopped and isn't in contact with the spring. So, our equation is reduced to:

`U_(gf)=U_(e0)\\\\U_(gf)=44.8J`

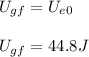
So, the gravitational potential energy of the block in its highest point is 44.8J.

c) Using the gravitational potential energy formula, we have:

`U_g=mgh\\\\\implies h=(U_g)/(mg) \\\\h=(44.8J)/((4.90kg)(9.8m/s^(2)) )=0.9m=90cm`

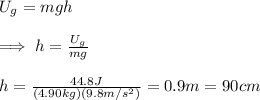
Using trigonometry, we can compute the distance between the release point and its highest point:

`d=(h)/(sin\theta)=(90cm)/(sin45\°)=127cm`