Question

In 2000 the population of a country reached 1 ​billion, and in 2025 it is projected to be 1.2 billion. ​(a) Find values for C and a so that ​P(x)equalsCa Superscript x minus 2000 models the population of a country in year x. ​(b) Estimate the​ country's population in 2010. ​(c) Use P to determine the year when the​ country's population might reach 1.4 billion. ​(a) Cequals nothing ​(Type an integer or decimal rounded to five decimal places as​ needed.)

Answer 1

(a) The value of C is 1.

(b) In 2010, the population would be 1.07555 billions.

(c) In 2047, the population would be 1.4 billions.

Explanation:

(a) Here, the given function that shows the population(in billions) of the country in year x,

`P(x)=Ca^(x-2000)`

So, the population in 2000,

`P(2000)=Ca^(2000-2000)`

`=Ca^(0)`

`=C`

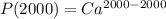
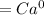
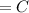
According to the question,

`P(2000)=1`

`\implies C=1`

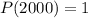
(b) Similarly,

The population in 2025,

`P(2025)=Ca^(2025-2000)`

`=Ca^(25)`

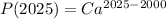
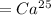
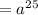`=a^(25)` (∵ C = 1)

Again according to the question,

`P(2025)=1.2`

`a^(25)=1.2`

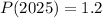
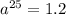
Taking ln both sides,

`\ln a^(25)=\ln 1.2`

`25\ln a = \ln 1.2`

`\ln a = (\ln 1.2)/(25)\approx 0.00729`

`a=e^(0.00729)=1.00731`

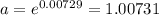
Thus, the function that shows the population in year x,

`P(x)=(1.00731)^(x-2000)` ...... (1)

The population in 2010,

`P(2010)=(1.00731)^(2010-2000)=(1.00731)^(10)=1.07555`

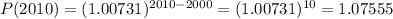
Hence, the population in 2010 would be 1.07555 billions.

(c) If population P(x) = 1.4 billion,

Then, from equation (1),

`1.4=(1.00731)^(x-2000)`

`\ln 1.4=(x-2000)\ln 1.00731`

`0.33647 = (x-2000)0.00728`

`0.33647 = 0.00728x-14.56682`

`0.33647 + 14.56682 = 0.00728x`

`14.90329 = 0.00728x`

`\implies x=(14.90329)/(0.00728)\approx 2047`

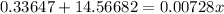
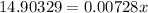
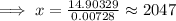
Therefore, the country's population might reach 1.4 billion in 2047.